16 Simultaneous Games

16.1 Introduction

We begin our study of creating and solving games by considering simultaneous games:

Players are tasked with predicting their competitors’ strategies without the benefit of observing their actions first. Simultaneity here means that all players make their decisions concurrently.
They choose strategies that encompass the comprehensive set of responses to every potential move a competitor might make. Thus, the focus shifts from reacting to actual actions to preparing for all conceivable ones.
They arrive at an equilibrium (expected outcome) where no players want to deviate because every player’s decision has been accurately forecasted and counteracted with the best response.

We will construct and analyze simultaneous games using the normal form representation, which organizes a game into a matrix format. This approach serves as an excellent foundation for understanding the core principles involved in creating and solving games. It’s essential for effectively applying game theory to real-world business challenges, offering a structured method to visualize and assess the strategic options and outcomes available to all players involved.

16.2 Pricing Game with a Single Nash Equilibrium

Let’s begin with a variation on the Prisoner’s Dilemma, tailored to an entrepreneurial context. Two startups, selling basically the same product through an online retail platform, are considering whether to cut prices to gain market share. The startups face the challenge of making their decisions in tandem, without the luxury of knowing the other’s choice ahead of time. The consequences of their decisions are heavily dependent on the combination of actions they each take, showcasing the strategic complexity and uncertainty inherent in competitive markets.

We build and solve the game working systematically through the five stages:

Step 1: Identify the Players

Players: The two competing startups contemplating price reductions are the players in this particular game:

Startup A (You), and
Startup B (Your Competitor).

Step 2: Outline Possible Actions

Actions: Each startup has two options:

to cut prices (Cut) or
to maintain current prices (Hold).

Step 3: Determine Payoffs

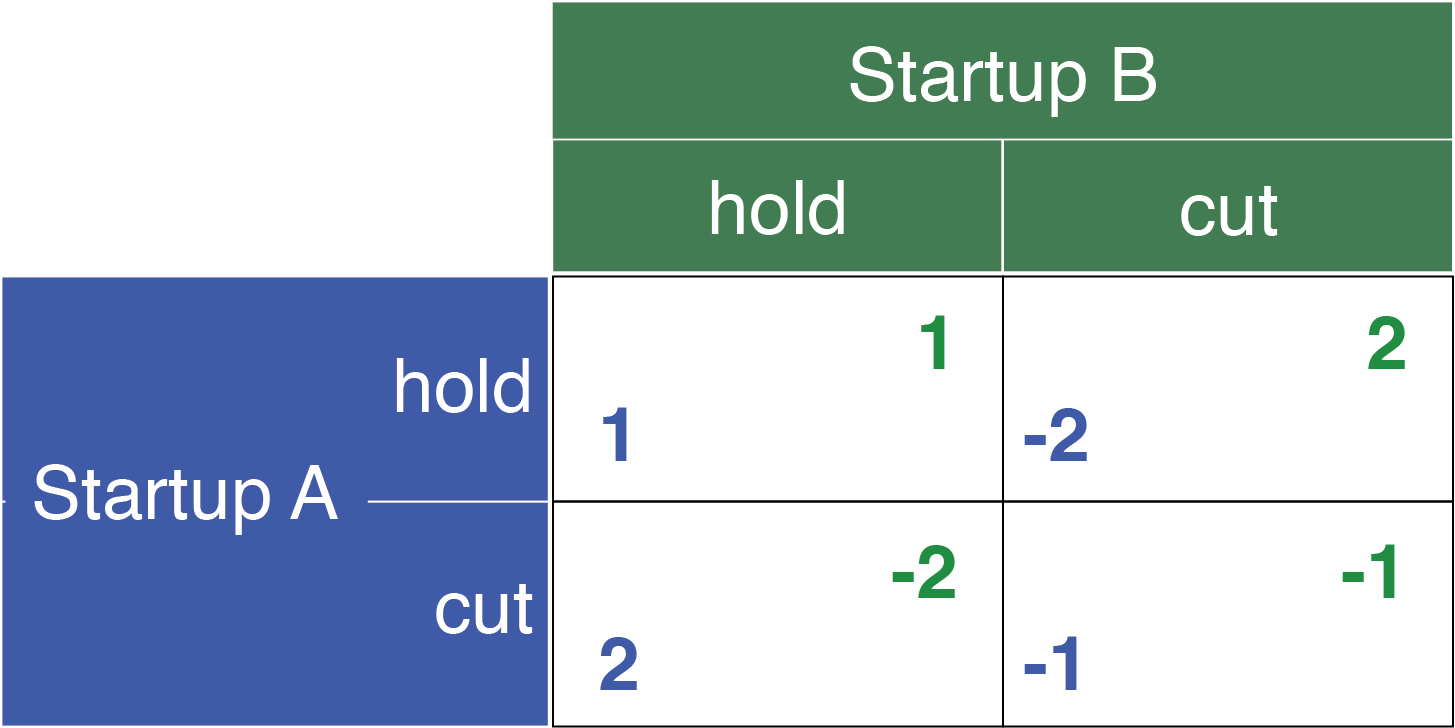
Payoffs represent the outcomes of different combinations of actions, defined here as ordinal values. These values rank the preferences of the players without specifying exact monetary benefits, where a payoff of 2 is more desirable than a payoff of 1, but is not necessarily twice as good.

When both choose to hold: Margins remain stable, leading to moderate gains for each, scored as a 1.
When one cuts while the other holds: The startup that cuts price captures additional market share, earning a payoff of 2, while the other, maintaining its prices, faces a disadvantage, incurring a payoff of -2.
When both decide to cut: a price war ensues, diminishing profits for both parties, reflected by payoffs of -1 each.

Armed with an understanding of the players, their possible actions, and the associated payoffs, we’re equipped to layout the game in a normal form matrix:

In this representation:

The “row player” (Startup A), shown in blue, faces the decision to hold or cut prices.
Similarly, the “column player” (Startup B), illustrated in green, navigates the same choices.
The matrix delineates the ordinal payoffs for Startup A (row player) in the bottom left of each cell and for Startup B (column player) in the upper right, corresponding to every possible action pairing.

This visual and structured approach to defining the game scenario illuminates the strategic interplay at hand, setting the stage for further analysis to discern optimal strategies and anticipate potential equilibrium outcomes.

Step 4: Identify Player Strategies

In game theory, a player’s strategy encompasses the suite of actions they would select as their best response to every potential move their competitor might make. An action qualifies as a best response when it secures the highest payoff among the available options.

For Startup A, strategic decisions hinge on Startup B’s pricing actions:

If Startup B opts to hold its prices, Startup A can maximize its benefit by cutting its own prices. This aggressive pricing strategy yields a higher payoff of 2, as opposed to the moderate gain of 1 that comes with maintaining price levels.
If Startup B cuts its prices, Startup A finds its most favorable outcome (-1) in reciprocating the price cut, aligning with Startup B’s aggressive strategy.

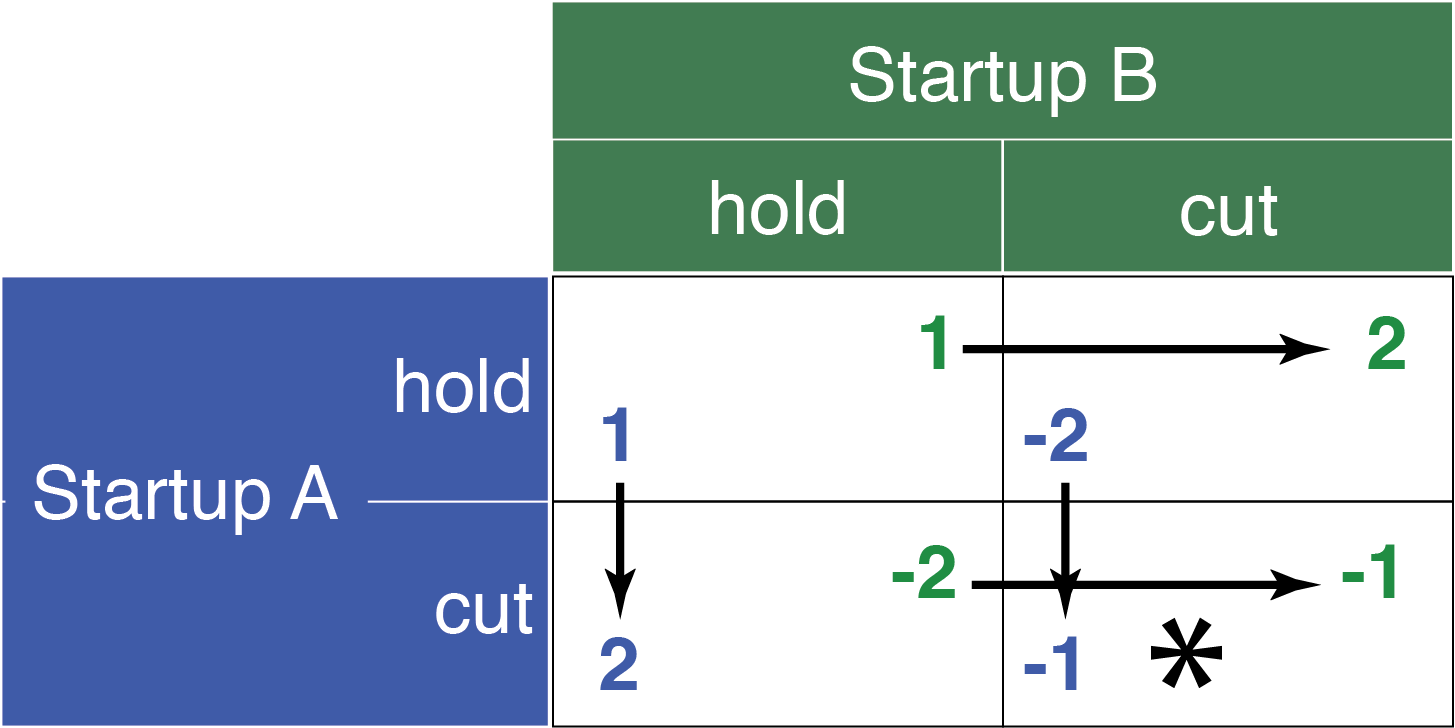
Startup A’s strategic pattern can be visually represented using directional arrows pointing towards actions yielding the highest payoffs, based on Startup B’s decisions.¹ As illustrated in Figure 16.2, both arrows for Startup A direct towards a price cut, indicating a strategy for Startup A to always opt for a price reduction, irrespective of Startup B’s choice.²

Startup B’s strategy mirrors this approach:

Facing a price hold from Startup A, Startup B’s advantageous move is to cut prices.
Similarly, when Startup A cuts prices, Startup B’s best strategy remains to cut, maintaining competitive parity.

This analysis reveals a pivotal insight: both startups are inclined towards a dominant strategy of price reduction under all circumstances, setting the stage for a potential price war. This is a normal form representation of undifferentiated Bertrand competition that eventually descends into price wars and zero profits. Such a scenario underscores the strategic intricacies inherent in competitive markets, where anticipating and countering the moves of rivals can define the contours of business success.

Step 5: Solve for Equilibrium

The Nash equilibrium³ is the strategic point where all players in a game settle on choices that leave them with no incentive to pursue a different course of action, provided that every other player remains constant in their strategy. This state of mutual best responses occurs when each player’s strategy is the best they can opt for, considering the strategies chosen by their competitors.

The game’s matrix, illustrated in Figure 16.3, highlights strategies through arrows pointing towards actions that garner the highest payoffs. The Nash Equilibrium is achieved when both startups opt to reduce prices, a strategy represented by arrows converging on the cut/cut decision. This scenario not only instigates a price war, diminishing profits for both entities but also exemplifies a dominant strategies equilibrium, where each firm’s unilateral decision to cut prices reflects the optimal response to the anticipated action of the other.

This real-world rendition of the Prisoner’s Dilemma epitomizes a broader class of strategic games where players, driven by dominant strategies, inadvertently converge on outcomes that might not serve their collective best interests. Through this lens, the dilemma doesn’t just offer a theoretical exercise but rather a practical reflection on the dynamics of competitive strategy, underscoring the critical importance of strategic foresight and the potential consequences of uncoordinated competitive aggression.

Practical Application: Navigating Competitive Strategy

The Prisoner’s Dilemma isn’t just a theoretical concept; it’s a vivid illustration of the strategic decisions entrepreneurs face daily. It highlights the importance of considering both the immediate impact of your actions and how competitors might respond.

Aggressive strategies, like price cuts, may offer quick wins but understanding the broader dynamics of competition can guide you towards strategies that ensure long-term market stability and profitability.

Mastering game theory’s principles, as demonstrated through the Prisoner’s Dilemma and its Nash equilibrium, empowers entrepreneurs to:

Forecast Competitor Behavior: Identifying dominant strategies helps predict competitor moves, giving you a strategic edge.
Look Beyond the Short Term: It encourages strategies that safeguard against potential market disruptions, favoring sustainable success.
Find Collaboration Opportunities: Understanding mutual dependencies can reveal partnerships that amplify your competitive advantage.
Clarify Decision-Making: Game theory models offer a clear visual framework to assess strategies and their outcomes, making complex decisions more manageable.

While pricing competition is a crucial element of game theory, entrepreneurs must consider a broader range of strategic interactions. Real-world business dynamics often involve multiple levers beyond simple price cuts. Here are some additional competitive responses that shape market positioning:

Competitive Responses Beyond Pricing

Entrepreneurs often compete on dimensions other than price. Some key alternative competitive responses include:

Marketing Campaigns: Startups may strategically allocate marketing budgets to influence consumer perception and demand. For example, a well-timed social media blitz or influencer partnership can capture attention and shift market share without resorting to price cuts.
New Product Launches: Firms may introduce differentiated products or expanded service offerings as a way to compete. Unlike price reductions, which erode margins, product innovation can create sustained competitive advantages.
Branding and Customer Loyalty: Strong branding can reduce price sensitivity among customers. Apple, for instance, maintains premium pricing due to its brand equity and loyal customer base.
Customer Experience and Service: Exceptional service, seamless user experiences, and personalized engagement can create differentiation that justifies premium pricing.
Product Differentiation: Unique features, superior design, or proprietary technology can shift competition away from pure price wars and toward value-based competition.
Exclusive Partnerships: Aligning with key distribution channels, supply chain partners, or complementary brands can provide an advantage that competitors may struggle to replicate.

These responses illustrate how strategic competition is more than just a pricing game—it involves actively shaping market dynamics through innovation, visibility, and differentiation. For startups, these strategies are especially valuable because they allow for growth without engaging in destructive price-based competition that erodes profitability.

Regulatory and Ethical Considerations

Entrepreneurs must also navigate the external constraints imposed by regulations and ethical norms. Game theory assumes rational decision-making, but legal and reputational factors often add complexity:

Regulatory Constraints: Price-fixing laws, antitrust regulations, and advertising restrictions can shape the feasible strategies available to startups. Understanding these legal considerations is crucial in competitive decision-making.
Ethical Considerations: Beyond legality, ethical business practices influence long-term success. Aggressive undercutting may generate short-term gains but damage brand reputation or invite retaliatory actions from competitors.
Industry Standards and Reputation: In some industries, informal agreements and industry standards may act as stabilizing forces, discouraging price wars and promoting cooperation.

These factors highlight that competitive strategy is not purely a mathematical exercise—it requires a nuanced understanding of external forces, incentives, and long-term consequences. By considering a diverse set of strategic responses beyond price cuts, entrepreneurs can position their businesses for sustainable success in competitive markets.

16.3 Strategic Partnerships to Address Multiple Equilibria

The dynamics of strategic partnerships often mirror those found in coordination games, characterized by the presence of multiple equilibria. These scenarios challenge firms to make decisions that not only serve their own interests but are also critical for the collective success of the alliance.

Imagine two startups, each with its own specialized technology, considering a strategic alliance. The effectiveness of their partnership is contingent on selecting operational standards or development trajectories that are mutually compatible. This decision-making process is akin to navigating a coordination game, where the most favorable outcomes are achieved through synchronized choices.

Identifying the Players and Actions

The players in this scenario are:

Startup A, with a specialization in software development,
Startup B, specializing in hardware production.

Their actions involve choosing between two operational standards or development paths: Standard X or Standard Y.

Determining Payoffs

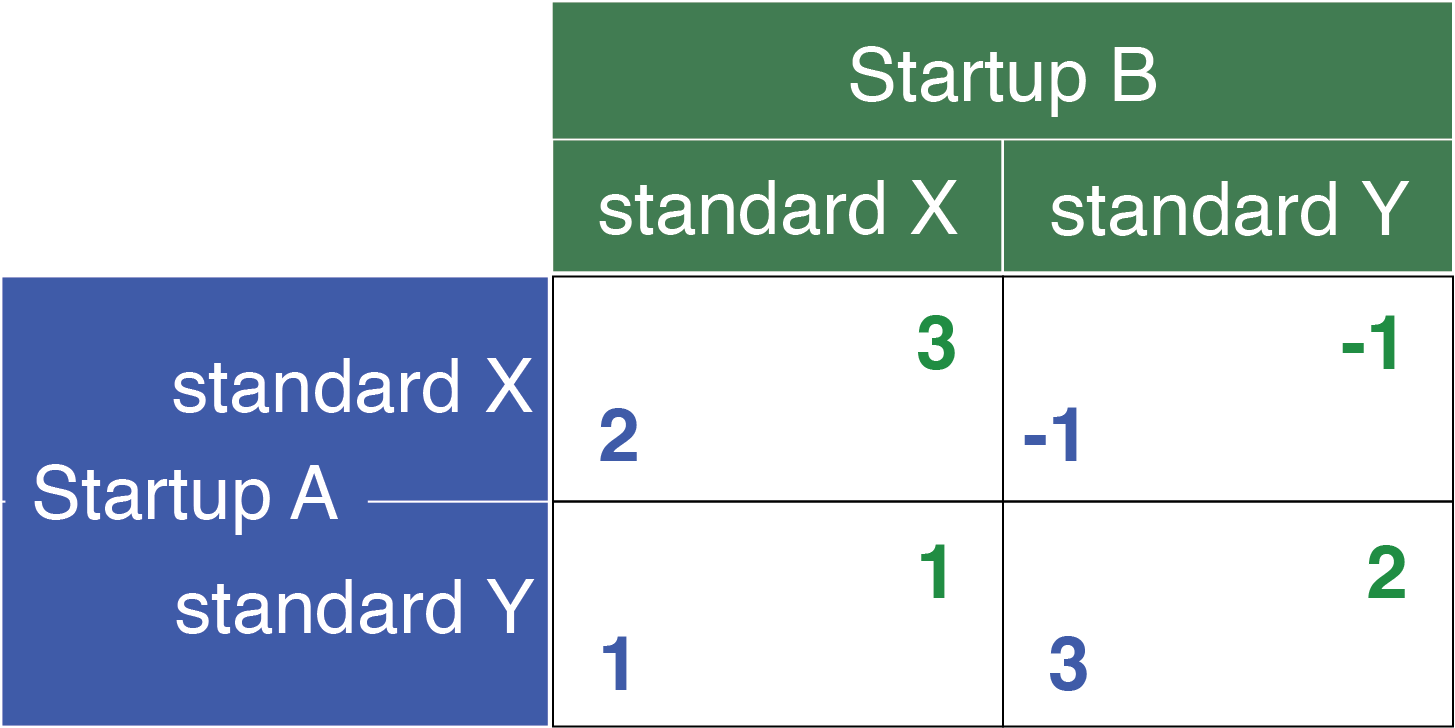
The payoffs reflect the compatibility of operational standards and the synergy effect on the partnership:

Both choose Standard X: High compatibility and synergy, leading to significant mutual benefits.
Both choose Standard Y: Similar to X, but with nuances that slightly favor Startup B’s hardware orientation.
Disparate choices lead to compatibility issues, diminishing the potential benefits of the partnership.

Constructing the Game in Normal Form

The game matrix, visualized in Figure 16.4, elucidates the outcomes based on the combinations of choices by the startups.

Strategy and Equilibria

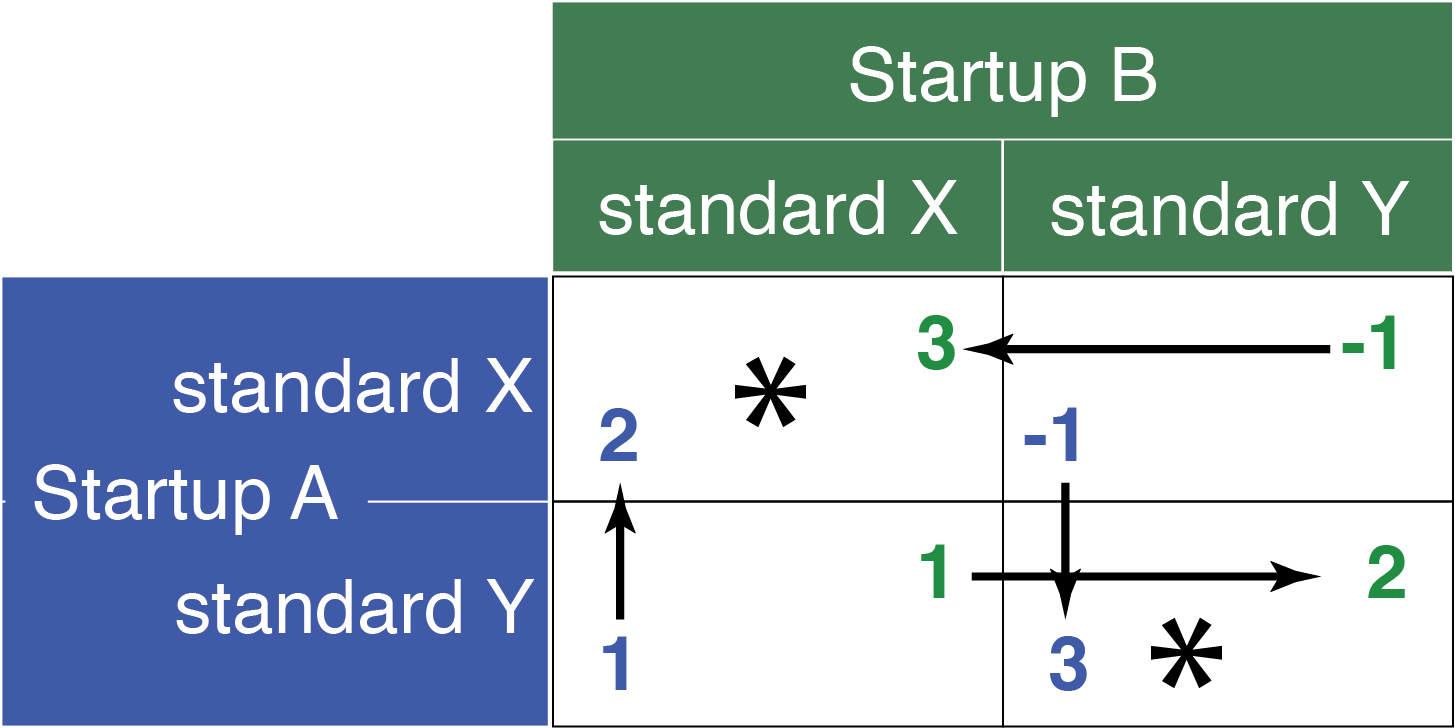
In this partnership game, both startups aim to align on a standard, understanding that compatibility maximizes the partnership’s value. The game is solved in Figure 16.5 where the presence of multiple Nash equilibria reflects the possible outcomes where each startup’s choice complements the other’s, ensuring mutual benefit.

Application to Strategic Partnerships

The presence of multiple equilibria in such a strategic decision-making context underscores the need for mechanisms that can guide the startups toward a single, mutually beneficial equilibrium. This could involve pre-negotiation agreements, shared vision sessions, or adopting a sequential decision-making approach where one startup’s choice informs the other’s decision, akin to moves in a sequential game.

Such strategies not only help align the startups’ decisions but also build a foundation for trust and cooperation, essential elements for the success of any strategic partnership. By effectively navigating these coordination challenges, startups can leverage their alliance as a competitive advantage, driving innovation and capturing greater market share.

Strategic partnerships, through the lens of game theory, reveal the complexities and opportunities inherent in collaboration. By understanding and applying the principles of coordination games, firms can more effectively navigate the intricacies of partnership dynamics, steering towards decisions that enhance both their individual prospects and collective success.

Strengthening Strategic Partnerships: Alliances and Coordination Mechanisms

Strategic partnerships are crucial in entrepreneurial settings, where startups often rely on collaborations to navigate resource constraints, enter new markets, or accelerate innovation. Unlike direct price-based competition, partnerships introduce coordination challenges, where multiple equilibria exist, and firms must align on mutually beneficial decisions.

Real-World Startup Alliances

In many industries, startups and incumbents must coordinate on technology choices, supply chain integrations, and market positioning. Some examples include:

Tech Stack and Platform Compatibility: Startups developing software or digital products often must align on technology choices to ensure interoperability. Choosing a cloud provider (e.g., AWS vs. Azure) or adopting an industry-standard API format can create coordination challenges, where an early misalignment can lead to costly integration issues.
Supply Chain and Logistics Partnerships: E-commerce startups may face coordination dilemmas in logistics. Partnering with a fulfillment provider like Amazon FBA or developing a direct-to-consumer (DTC) logistics network each presents strategic trade-offs that impact long-term efficiency.
Industry Ecosystems and Standardization: Some industries rely on agreed-upon protocols to ensure compatibility. For example, electric vehicle (EV) startups must decide whether to adopt Tesla’s charging standard or align with broader industry standards like CCS (Combined Charging System).

In each case, multiple equilibria exist, and firms must navigate these coordination dilemmas to ensure mutual success.

Pre-Negotiation and Commitment Mechanisms

Coordination games often suffer from equilibrium selection problems—there may be multiple stable outcomes, but the challenge is ensuring all players choose the same one. Entrepreneurs can use commitment mechanisms and pre-negotiation strategies to resolve these dilemmas.

Pre-Negotiation Agreements: Before finalizing strategic choices, startups can engage in pre-negotiation discussions to align expectations. For example, a startup entering a new market may negotiate distribution partnerships ahead of time to signal commitment to a particular channel.
Public Commitments and Announcements: Declaring a choice publicly can serve as a strategic commitment. For instance, when Apple announces support for a particular wireless standard or payment technology, it influences suppliers and app developers to follow suit.
Long-Term Contracts and Exclusivity Deals: Startups can lock in key partnerships through contractual commitments. An early-stage fintech company might secure an exclusive banking partnership to create a stable foundation before competitors can respond.
Regulatory or Industry-Guided Standardization: Sometimes, external entities help resolve coordination issues. Government policies or industry consortia (e.g., the USB-IF for USB standards) can enforce a particular equilibrium, reducing strategic uncertainty.

By leveraging commitment mechanisms, startups can guide competitors, suppliers, and partners toward an outcome that maximizes collective benefits rather than leaving the equilibrium selection to chance.

Application to Entrepreneurial Strategy

Understanding coordination games enables entrepreneurs to: - Recognize when collaboration is more beneficial than competition. - Influence equilibrium selection through pre-commitment and strategic signaling. - Avoid misalignment pitfalls that increase costs or reduce market opportunities.

As markets evolve, game theory provides entrepreneurs with powerful tools to structure alliances, negotiate agreements, and shape industry standards. Mastering these concepts allows startups to gain competitive advantages not just through direct competition, but by strategically orchestrating partnerships that define the future of their industries. “)

16.4 Navigating Uncertainty with Mixed Strategies: Rock-Paper-Scissors

Rock-paper-scissors, beyond being a childhood game, exemplifies strategic decisions in scenarios lacking a clear Nash Equilibrium. This game illustrates that sometimes, business strategies don’t lead to straightforward outcomes and that embracing flexibility and unpredictability can be advantageous.

Constructing the Game

In constructing payoffs for rock-paper-scissors, we use ordinal payoffs to signify preferences rather than exact values. For instance, tying might have a payoff of 0, a win 1, and a loss -1, setting a baseline for evaluating outcomes. The formal game is represented in Figure 16.6.

Solving the Game

The solution to the rock-paper-scissors game is given in Figure 16.7 with curious results. The strategies of both players are not hard to find but there is no Nash equilibrium. Analysis reveals no single strategy guarantees a win, because there is every cell has an arrow leaving meaning that there is no outcome that is simultaneously a best response for both players. When you build and solve bespoke games for your context, you may not find a pure strategies equilibrium.

Mixed-strategies Equilibrium

When the game has no Nash equilibrium, you may turn to the concept of mixed-strategies, randomizing decisions for direction in decision-making. The problem for players of rock-paper-scissors is that any action can be countered with an action that will always win. It doesn’t take long for players (often children) to learn that they must randomize their choice or they will always lose. If they place $\mathsf{\frac{1}{3}}$ probability on each choice to avoid predictability, they will lose one-third of the games, win one-third, and tie one-third.

This approach is a mixed-strategy and leads to a mixed-strategies equilibrium. It does not tell you what action to take but it does help you choose randomization. The equilibrium does not allow us to predict the outcome that will happen but it does predict the the probability of any outcome. This is an equilibrium because no player has an incentive to deviate.

This approach underscores the importance of adaptability and the potential to incorporate randomness into strategic planning, especially in highly competitive or uncertain markets. While Rock-Paper-Scissors is a simple illustrative example, mixed strategies play a significant role in high-stakes entrepreneurial and strategic decisions.

Real-World Examples of Mixed Strategies in Entrepreneurship

Entrepreneurs and startups frequently encounter situations where randomization is an optimal strategy:

Online Advertising Bidding Wars: Many digital advertising platforms (e.g., Google Ads, Facebook Ads) operate on auction-based pricing models. If a company repeatedly bids on the same keywords with a fixed strategy, competitors can exploit this predictability to drive up costs. A mixed strategy—randomly varying bid amounts and timing—prevents being undercut or outmaneuvered by rivals.
Startup Funding and Investor Competition: In venture capital (VC) funding rounds, investors must decide which startups to back, and startups must strategically signal their valuation. If a VC always follows the same decision criteria, founders can game the system. A mixed-strategy approach (diversifying investments across different verticals or adjusting deal structures probabilistically) can mitigate bias and enhance portfolio resilience.
Competitive Pricing in Dynamic Markets: Ride-sharing companies like Uber and Lyft often adjust pricing dynamically based on supply and demand. If pricing were static, competitors could respond predictably, leading to price wars. Instead, using mixed strategies—varying price surges and discounts unpredictably—helps maintain profitability while avoiding exploitative competitor behavior.
Cybersecurity and Fraud Prevention: Online platforms must prevent fraudulent activities and cyberattacks, yet attackers adapt quickly to static defenses. By randomizing fraud detection measures or security updates, companies create an unpredictable barrier that makes it harder for adversaries to anticipate vulnerabilities.

Probabilistic Decision-Making in Entrepreneurship

Entrepreneurs often operate under high uncertainty, where traditional deterministic decision-making is insufficient. Mixed strategies provide a systematic way to embrace uncertainty and optimize decisions probabilistically.

Avoiding Exploitable Predictability: If competitors, customers, or investors can perfectly anticipate a startup’s next move, they may exploit this knowledge. Introducing randomness into pricing, promotions, or feature rollouts can prevent strategic manipulation.
Balancing Risk and Innovation: Startups frequently face choices between pursuing a risky innovation or a safer, incremental improvement. By allocating resources probabilistically—testing multiple ideas in parallel or investing in a mix of short-term and long-term projects—entrepreneurs hedge against failure while maintaining innovation momentum.
Market Entry and Expansion Timing: Startups entering new markets must decide when to launch. If competitors can predict the exact timing, they may preemptively launch competing products or block access to key suppliers. A mixed-strategy launch schedule, with staggered or randomized market entry timing, can help mitigate competitive responses.

Strategic Benefits of Mixed Strategies

Entrepreneurs leveraging mixed strategies can:

Disrupt competitor expectations by making decisions less predictable.
Optimize decision-making under uncertainty, particularly in zero-sum or adversarial markets.
Enhance long-term resilience by diversifying strategic actions rather than relying on a single deterministic path.

Mastering mixed strategies allows entrepreneurs to thrive in uncertain and competitive environments, leveraging probabilistic thinking to gain strategic advantages in dynamic markets.

16.5 Build Custom Games

Diving into the practical application of game theory, we aim to equip you with the ability to craft and solve games tailored to the unique strategic challenges of your business environment. This approach ensures that insights are directly applicable, guiding you toward informed strategic decisions in real scenarios.”

A pivotal step in applying game theory is defining payoffs—the outcomes of strategic decisions. We’ll explore both ordinal and cardinal payoffs: ordinal payoffs simplify strategic preferences without specific values, offering a clear view of options, while cardinal payoffs provide a detailed, quantitative analysis of decisions’ impacts. By mastering these methods, you’ll be equipped to use game theory effectively, leveraging strategic insights for competitive advantage.

Ordinal Payoffs: A Logical Approach

Identifying payoffs is a crucial yet challenging step in game theory, particularly when the strategic scenario defines players and actions clearly, but payoffs remain ambiguous. For ordinal payoffs, the key is to ensure they represent a clear ranking of outcomes without necessitating specific values or units. Start by selecting a baseline scenario and assigning payoffs that mirror the expected order of preferences. For instance, in a rock-paper-scissors game, a tie scenario like Rock/Rock might be assigned a payoff of 0/0. This sets a foundation to then value a win at one point and a loss at negative one, simplifying the construction of the game matrix based on these relative rankings.

Ordinal payoffs expedite game building by sidestepping detailed financial calculations, provided they accurately reflect the preference order. By methodically considering the relative merits of different strategic outcomes, you not only craft a clearer game structure but also enhance your strategic insights, enabling informed decision-making and predictable outcomes.

Cardinal Payoffs: A Competition Analytics Approach

While ordinal payoffs rank outcomes based on preferences, cardinal payoffs require quantifiable insights often not evident through mere speculation. These payoffs, crucial for understanding the tangible outcomes of strategic choices, are derived from profit analytics. Whether it’s profits from a one-time differentiated Bertrand competition or the net present value (NPV) of ongoing competitive profits, cardinal payoffs quantify the financial impact of decisions over the duration of interdependence between players. This depth of analysis, rooted in profit calculations, provides a comprehensive view of potential strategic outcomes.

A Demonstration Case of Airbus and Boeing Choosing to Develop a New Aircraft

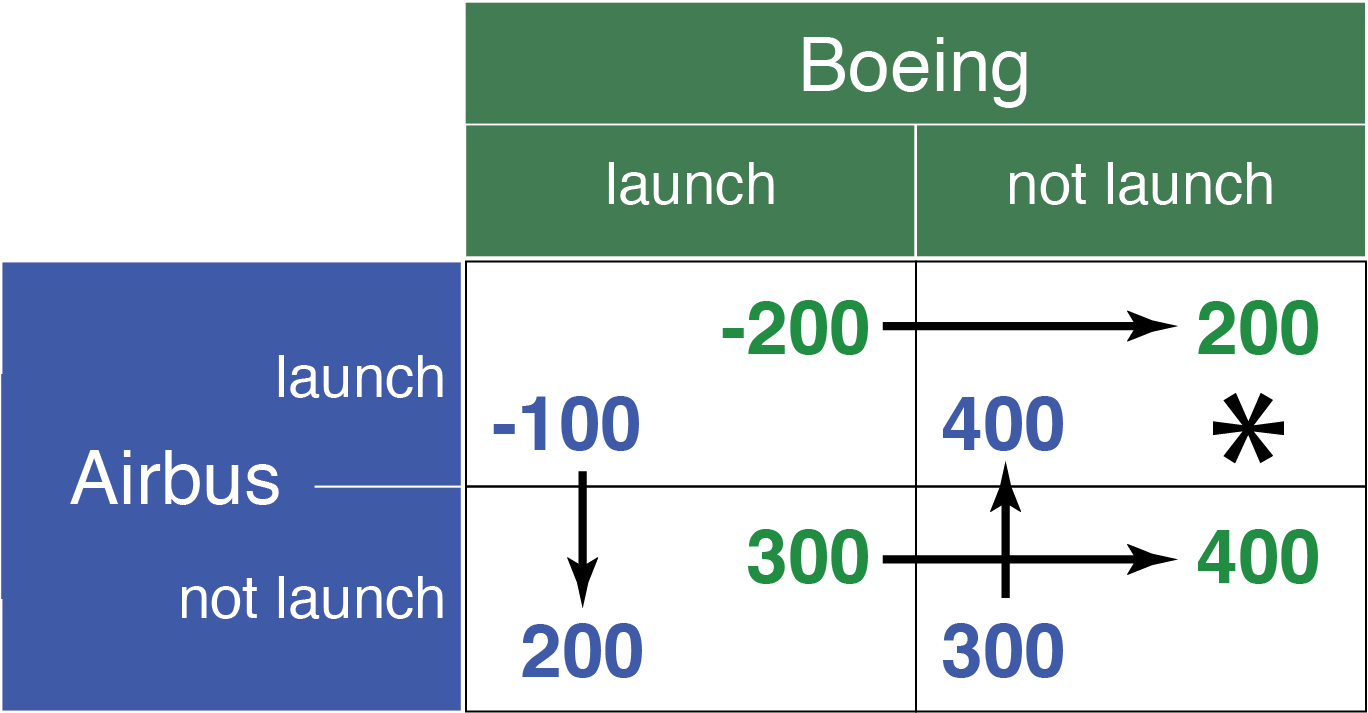
Consider Airbus and Boeing, evaluating whether to develop a new, technologically advanced aircraft. This strategic decision is influenced by potential market responses, competitive actions, and financial implications. Here’s how we break down their game using cardinal payoffs derived from profit analytics.

Players: Airbus and Boeing

Actions: Each can either Innovate or Not Innovate.

Payoffs: Derived from a discounted cash flow (DCF) analysis, reflecting the net present value (NPV) of the calculated Bertrand oligopoly profits over 20 years. These are hypothetical yet realistic figures based on competitive analytics and demand forecasts:

Both not innovate: Airbus NPV = $30B; Boeing NPV = $40B.
Airbus innovate, Boeing not innovate: Airbus NPV = $40B; Boeing NPV = $20B.
Boeing innovate, Airbus not innovate: Airbus NPV = $20B; Boeing NPV = $30B.
Both innovate: Airbus NPV = -$10B; Boeing NPV = -$20B.

The determination of these payoffs involves extensive data collection and demand analysis. For instance, we estimate demand curves for each scenario, accounting for variable and fixed costs—including R&D investments. This process, while data-intensive, is crucial for major strategic decisions that could define the company’s future.

Strategies and Equilibrium:

The game matrix, illustrated in Figure 16.8, reveals that Boeing has a dominant strategy not to innovate, allowing Airbus to launch the new aircraft and secure an enhanced competitive position in the advanced technology market.

This example underscores the significance of grounding strategic decisions in solid analytics. While ordinal payoffs offer quick strategic insights, cardinal payoffs provide the depth necessary for high-stakes decision-making, ensuring strategies are not just intuitive but analytically sound.

16.6 Conclusion

Strategic Decision-Making in Competitive Markets

Simultaneous games provide a foundational tool for understanding competition. Entrepreneurs must anticipate and counter rival moves, often without knowing their strategies in advance. Through normal form representation, we can model strategic interactions and identify Nash equilibria that reveal stable competitive outcomes.

However, real-world business decisions extend beyond simple price wars:

Some markets involve coordination dilemmas, where firms must align on standards or collaborate.
Others require randomized strategies to avoid predictability in adversarial settings.
Entrepreneurs can shape outcomes by leveraging commitments, pre-negotiations, or differentiating their offerings.

Mastering game theory enables entrepreneurs to outthink competitors, recognize exploitable patterns, and anticipate market dynamics. As we transition into sequential games, we will see how timing, commitment, and foresight can further refine strategic decision-making.

There are many ways to represent normal form games and their payoffs and strategies. None seems to be be completely superior. Thomas Schelling, 2005 Nobel prize winner in economics, introduced this method of placing payoffs in the corners of each cell and using arrows to describe best responses. The best-response arrows are cousins to the reaction functions we saw in Bertrand oligopolies.↩︎
When the best response of one player is always the same action, like Startup A choosing to cut price in both cases, that player has a dominant strategy.↩︎
John Nash won a Nobel prize in economic sciences for his research on the problem of bargaining over the value created through cooperation (Nash 1950). If a group collaborates to create new value, how should they split the value? Nash overcame the mathematical “indeterminacy” that was a roadblock to earlier mathematicians by focusing on individuals that choose their best response to the choices of others (Nash 1951).↩︎