17  Sequential Games

17.1 Introduction

In many situations, the assumption that all companies act at the same time strains credibility. Many real-world strategic decisions unfold in a sequence rather than all at once. In sequential games, players make their moves one after another, allowing later players to react to the decisions of those who acted before them. This sequence of moving and responding fundamentally changes the game’s dynamics and treating them like a simultaneous game leads to flawed strategies and disappointing outcomes.

For example, in a coordination game like the battle of the sexes, if one of the players chooses a venue first, the other can respond only to that venue. In this case, one of the equilibria disappears and the reasonable risk of the worst outcome is eliminated. More generally, making the assumption that games are played simultaneously when they are actually played in sequence leads to incorrect strategies and uncertain equilibria.

17.2 Non-Credible Threats

In sequential games, the timing and order of decisions are not insignificant details. The ability to observe and react to a competitor’s move can be a significant strategic advantage. The ability to anticipate a competitor’s response allows players to move pre-emptively and shape the competitive environment in their favor. Moving first, for example, allows a firm to make strategic commitments that can deter competitors, secure resources, or lock in advantageous positions by forcing competitors to respond to the early mover on less favorable terms.

In sequential games, the dynamics go beyond mere observation and response. They open up the possibility of non-credible threats, where a player might threaten to take actions that, upon closer inspection, wouldn’t actually be in their interest to carry out. Such threats, lacking in credibility, should typically be ignored, as they’re unlikely to be acted upon. Distinguishing between credible and non-credible strategies becomes a critical skill in navigating the strategic landscape of sequential games.

Thankfully, the challenge of identifying and countering non-credible threats can be systematically addressed by constructing the game in an extensive form (essentially, a decision tree) and solving it through backward induction. This method for identifying strategies, simplifies the analysis by breaking down the game into a sequence of decisions to choose the best response, starting from the end and working backwards. By doing so, it becomes evident which threats or actions are actually in a player’s interest to follow through on, based on the outcomes of subsequent moves.

This method not only clarifies which strategies are credible but also enhances strategic planning and decision-making. It allows entrepreneurs and strategists to anticipate competitor moves more accurately, devise responses that effectively counter non-credible threats, and leverage their own strategic moves for maximum impact. Through the use of extensive form games and backward induction, the complex interdependencies of sequential decisions become navigable, empowering businesses to craft strategies that are both informed and actionable.

17.3 Constructing Seqential Games in Normal Form

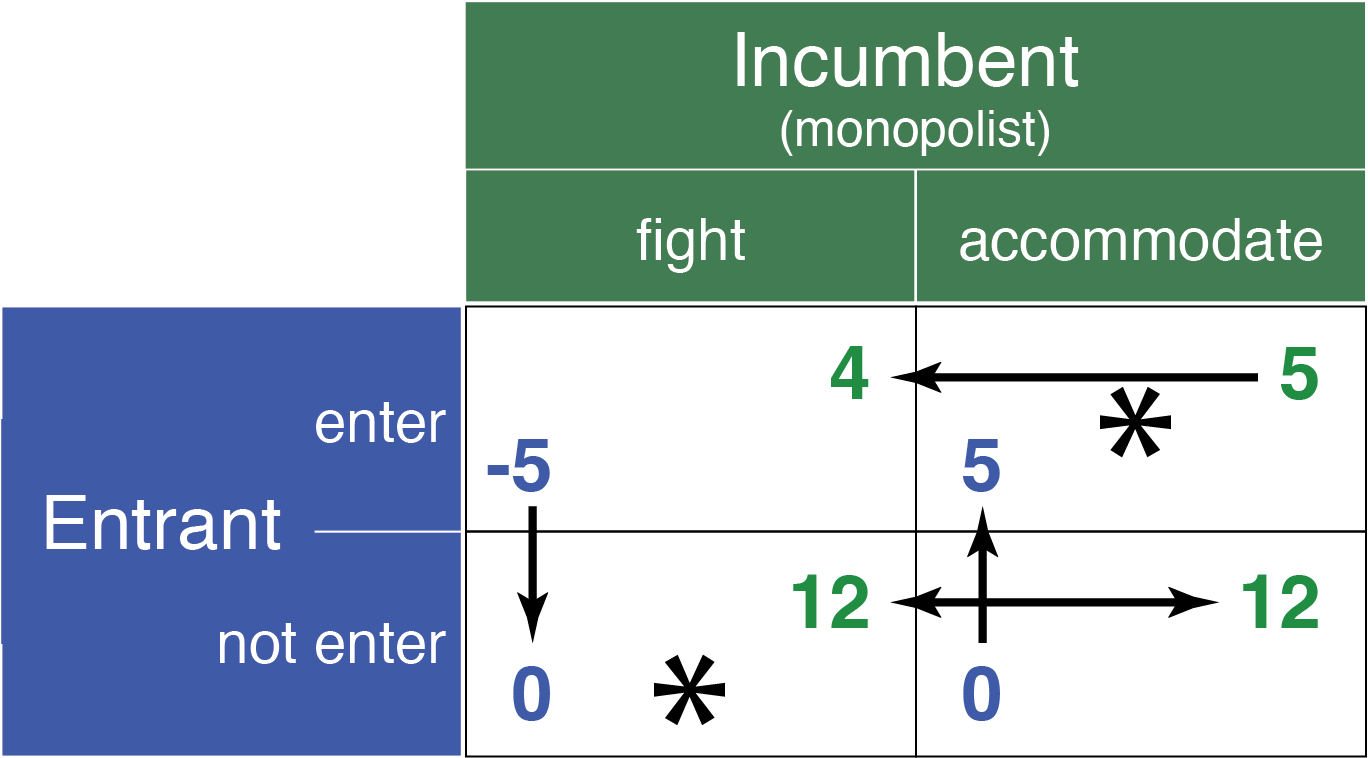
Consider a simple game where an entrepreneur deliberates entering a market dominated by a monopolist. The entrepreneur’s choices are to enter or not enter, while the monopolist can fight the entry with aggressive pricing or accommodate by sharing the market. The outcomes are quantified as follows:

• Enter and fight: The entrepreneur faces a $5M loss, while the monopolist gains $4M.
• Enter and accommodate: Both parties profit by $5M each.
• Not enter: Regardless of the monopolist’s choice, the entrepreneur gains nothing, and the monopolist secures a $12M profit.

Solving this game in normal form reveals two Nash equilibria seen in Figure 17.1: one where the monopolist fights and deters entry, and another where the entrant enters and is accommodated. But which outcome is more likely?

Figure 17.1: If the entry game is played simultaneously in normal form, the solution is two Nash equilibria where the monopolist may fight or accommodate and the entrant may enter or not enter.

Given the logical sequence of moves, the entrant must decide first, providing the monopolist with something to fight or accommodate. This sequential decision-making highlights the non-credibility of the monopolist’s threat to fight. If the entrant chooses to enter, knowing the monopolist’s best interest lies in accommodating, the threat of a price war becomes ineffective. This realization negates the not enter/fight equilibrium, leaving enter/accommodate as the most plausible outcome.

The crux of sequential games is recognizing that threats lacking in credibility—those not in a player’s best interest to execute—should not influence decision-making. The sequencing of moves clarifies which strategies are bluffs and which are genuine, guiding players towards rational and beneficial outcomes. This principle is pivotal in strategic environments where timing and order of actions shape the competitive landscape, enabling players to navigate complex scenarios with foresight and precision.

17.4 Constructing Sequential Games in Extensive Form

When dealing with sequential-move games, particularly those with multiple stages, constructing them in extensive form enhances clarity. This format visualizes the game as a decision tree, where nodes represent decision points for players, and branches indicate possible actions.

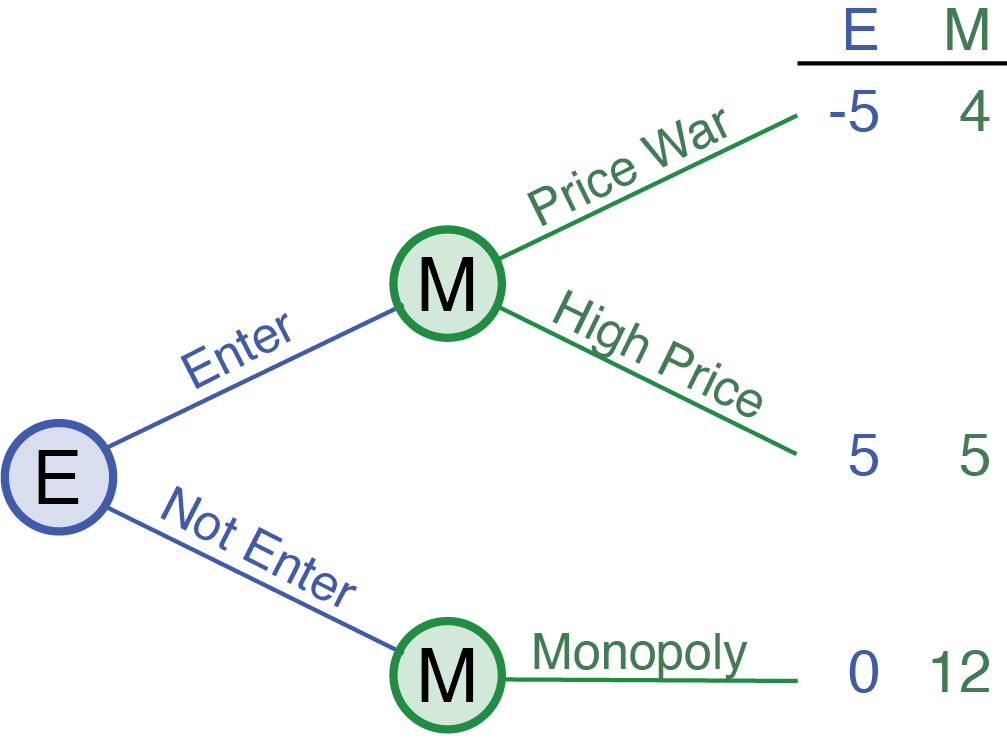
For illustration, let’s revisit the monopolist-entrant game, now depicted in extensive form as seen in Figure 17.2. In this decision tree:

• “E” marks the entrant’s decision node: to enter or not enter.
• “M” nodes represent the monopolist’s subsequent choices: to fight by initiating a price war or to accommodate by maintaining high prices and sharing the market.

The payoffs, aligned with our previous discussion in normal form, are noted at each terminal node, reflecting the outcomes of combined actions. The arrangement of payoffs (whether on the left or right) should maintain consistency and clear labeling to avoid confusion.

Figure 17.2: Construction of the entry game with sequential moves in extensive form: “E” is the entrant, “M” is the monopolist, their possible actions are marked on the paths, and their payoffs are given at the end of each decision path.

Solving Sequential Games Through Backward Induction

To solve sequential games in extensive form, we use a method known as backward induction, which clarifies the decision-making process by working from the game’s end back to its start. This method helps us pinpoint the best response at each decision point, considering the subsequent moves of other players.

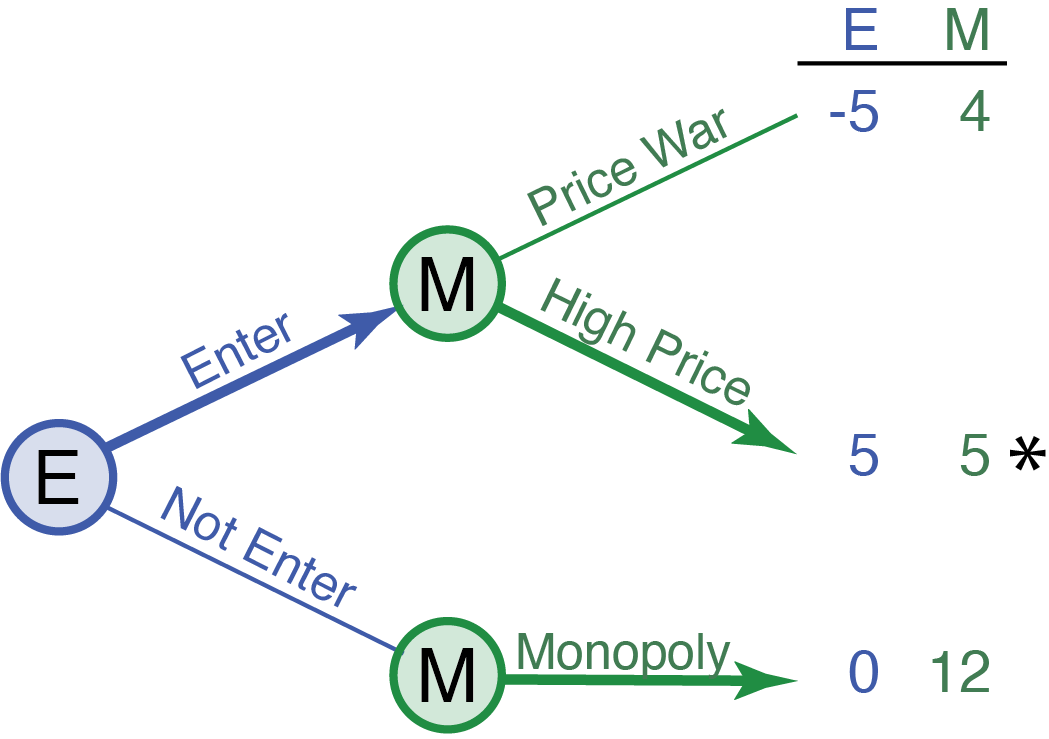
Returning to our monopolist-entrant game in extensive form, we start with the monopolist’s final decisions. Given the choice between a price war and maintaining high prices after the entrant has entered, the monopolist prefers the latter, yielding a higher payoff. This preference is represented in Figure 17.3 by a bolded arrow towards the high price decision, indicating the monopolist’s best response. When the entrant does not enter, we move to the lower node for the monopolist where it retains monopoly status regardless of whether if fights or accommodates.

Figure 17.3: Solving the entry game in extensive form through backward induction: best responses are indicated by bolded arrows, leading to the sub-game perfect equilibrium.

The entrant, considering the monopolist’s response, finds entering the market to be the best move, given it leads to a mutually beneficial profit sharing. This decision path is marked, leading to the game’s equilibrium point, where both firms play their best responses simultaneously.

The key outcome of backward induction is the sub-game perfect equilibrium, which inherently discounts non-credible threats. Unlike in our initial normal form game, where the monopolist’s threat of a price war might deter entry, sequential analysis reveals such threats as non-credible. The monopolist, in reality, would choose to accommodate entry, rendering the price war strategy implausible when actions unfold over time.

Thus, the sub-game perfect equilibrium identified through backward induction is a refined Nash equilibrium specific to sequential games.¹ It focuses on credible strategies by considering the actual sequence of moves, ensuring that only feasible outcomes—those based on rational, best-response strategies—are considered viable. In doing so, it sidesteps the ambiguity of non-credible threats found in simultaneous-move games, offering a clear pathway to strategic decision-making in real-world scenarios.

Entrepreneurial Applications: First-Mover vs. Second-Mover Advantages

In business strategy, sequential decision-making shapes market outcomes by determining who moves first and how competitors react. Understanding whether to act early or wait can make or break an entrepreneurial venture.

First-Mover Advantages

A first mover in a new market may benefit from:

• Brand Loyalty & Market Share: Early movers often establish customer loyalty before competitors enter.
• Cost Leadership: By scaling operations early, a first mover may drive down costs, making it harder for later entrants to compete.
• Network Effects: In industries like social media or fintech, early adopters create self-reinforcing user bases that discourage switching.

However, first movers also face risks:

• They bear the cost of educating customers, while later entrants benefit from an already established market.
• Competitors can reverse-engineer innovations and introduce superior products.
• Unproven markets may lead to costly failures (e.g., early AI startups that ran out of funding before the market matured).

Second-Mover Advantages

Not all advantages go to first movers. Second movers can:

• Learn from first-mover mistakes and refine their product accordingly.
• Enter with better technology after observing customer reactions.
• Compete on cost efficiency by avoiding the heavy R&D expenses faced by pioneers.

For example, Facebook was a second-mover in social networking, learning from Friendster and Myspace’s missteps before dominating the space.

For entrepreneurs, recognizing whether their business is a first-mover advantage play (like Tesla in EVs) or a second-mover strategy (like Apple refining smartphones after Blackberry) is critical for effective strategic planning.

17.5 Conclusion: Strategic Thinking in a Sequential World

Sequential games provide a critical framework for understanding how timing and order influence strategic outcomes. Unlike simultaneous games, where competitors move blindly, sequential games allow firms to observe, anticipate, and react—making strategic foresight a key advantage.

Key Takeaways

• First-mover vs. second-mover strategies define how businesses enter and compete in markets.
• Commitments and threats must be credible to be effective—rational competitors ignore bluffs.
• Backward induction is a powerful tool for identifying the most realistic equilibrium and avoiding bad strategic choices.

By applying these concepts, entrepreneurs can make better strategic decisions, avoid predictable pitfalls, and use timing as a competitive advantage. Whether launching a new product, expanding into a new market, or deterring competition, understanding sequential decision-making is a fundamental skill in entrepreneurial strategy.

---

1. All sub-game perfect equilibria are Nash equilibria but the inverse is not true.